Comments by GerdDegens
An extension in your sense is not the subject of discussion.
You can certainly scrap the entire concept. Agreed, but which concepts in the CVP stand up to your inspection?
Mind games should be able to be discussed. Or do you have a different opinion?
Diagonal movement is allowed through the corners of spaces that do not share any sides, and diagonal movement in the same direction goes through the corners at opposite ends of spaces.
Let me understand this correctly: A bishop on e8 moves in the direction of switch A4/a4. Further down in your description you say that in this case the bishop can only reach A4. But the bishop reaches the same corner of A4 and a4; therefore the bishop can decide whether to stop on A4 or a4.
So, in principle, a move into the switch, no matter from which direction and valid for all pieces, must result in a decision between the two squares of the switch - provided that the switch is not occupied.
My description for this is:
- Finally, you can move into a switch from below, from the side or from above. If the switch is not occupied, then you can choose whether the piece that moves into the switch is on 4 or a4 or 5 or h5 after the move. If the switch is occupied, then the piece in the switch must be captured; the opponent’s piece takes the place of the captured piece.
2. While some paths can lead to either Switch, others lead to only one space or the other in a Switch. For example, a Bishop on e8 can go to A4 or h5, and a Bishop on d1 can go to a4 or H5.
See the comments above.
A bishop on e8 or d1 can move to A4 or a4 respectively to h5 or H5.
Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
But a bishop on A4 cannot move to f8. For that he would have to be on a4.
3. ... or one is occupied by an enemy piece. If a piece moves to the empty space in a Switch, and the other space is occupied by an enemy piece, that piece is considered captured.
A piece can only be captured on the square it stands. Therefore, in an occupied switch, you cannot move to the empty square and capture the piece on the other square of the switch. After the move into the occupied switch, the capturing piece stands on the square of the captured piece.
The Knight can leap directly to any space that could be reached in two one-space moves except for those reachable by two in the same direction.
I am not sure if the rule is correct. In my description I use a definition which comes from Alfred Pfeiffer (Chemnitzer Schachverband e.V.):
- The knight moves to one of the squares that a king can reach from the square in two moves, but which are not on the same row, line or diagonal. It does not move across squares that lie in between.
No, it cannot. Let me break the move down into steps. First, the Bishop on e8 moves to d7. At this point, movement in the same direction must go through the opposite corner is just passed through. This is the corner that d7 shares with c6. Continuing in the same direction, it can go to b5. At b5, it can move diagonally to A4, because b5 and A4 share a corner but no sides. Also, this is in the same direction that the move from e8 to b5 was in. However, b5 and a4 do share a side, which means that movement from one to the other is not diagonal. So, a move from e8 to a4 would be illegal.
This is a very special consideration. Do you think that such can be communicated to potential players?
Why do we leave out consideration of equal/different corners and sides? Can't we agree that switches can be entered from all sides and a choice must be made between the fields of the switch? Surely that would be much easier for everyone.
In the discussion at the time, I just took your position, but ran into a wall looking for a simple solution. I came to the conclusion that switches have a special status, which must lead to a choice between the fields of a switch from all sides - from above, from below and from the side.
No, that is completely the opposite of how I understand the rules.
A bishop on e8 or d1 can move to A4 or a4 respectively to h5 or H5.
This is unintelligible. If you mean what you said above, it is contrary to my understanding of the rules.
What can I say? I think my position is quite logical. At the beginning of the discussions, I was of the opinion that switches work differently when they are operated from below, from the side, or from above. I have abandoned this opinion and changed it in favor of a pragmatic solution, in that a switch must be handled the same regardless of the direction.
Are you saying that a piece cannot capture a piece in a Switch unless it can move to the space the piece is on? Or are you saying that when a piece can move to either space in a Switch, it can move to the Switch and capture the piece, and then it must occupy the space the piece was on?
This seems to me to be much simpler than you make it out to be.
After all, a piece can only be captured where it is. Why should this be different for a switch?
Why should a piece be able to move to A4, and thereby capture a piece on a4 quasi en passent? That only happens with pawns. But that's where it should stay. The basic principle should be that pieces are captured on the square on which the pieces were placed. Pragmatic solution, isn't it?
They are the same, but I removed the ambiguities in his description and used some technical language. Since the King cannot move into check, and a Knight is not subject to the same restriction, I replaced the reference to two King moves with one to two one-space moves. Since I would normally refer to ranks and files rather than to rows and lines, and since I have been using these words in an algebraic sense rather than a geometric sense, I rewrote it to not use them. To "leap directly" is technical terminology that implies that a move "does not move across squares that lie in between."
I think I have understood that.
...because paths to and from Switch spaces are no longer symmetrical with each other. This would allow one King to attack another, and the following position would count as checkmate.
I can't see anything other than a checkmate situation. The legal moves of the black king are vertically a5 and a3, horizontally b4 and diagonally b5 and b3. The move to c5 is excluded and only with that can the black king free itself.
We had such a situation in the discussion below and it involved a bishop on A4.
Also, a Bishop on A4 can move away on either light or dark spaces, but one on a4 can move away only on light spaces.
But a bishop on A4 cannot move to f8. For that he would have to be on a4.
That is correct, and I didn't say anything to the contrary. The light path from A4 goes through b3, c2, and d1.
If the bishop on A4 cannot move towards f8, then the king on A4 cannot move to c5? On the other hand, the white king can capture the black king on A4. This is undoubtedly an asymmetry that, as I understand it, cannot be avoided when handling a switch.
I guess I didn't understand your question correctly. I'll try my best to answer.
The switch is occupied, so the black pawn can move diagonally into the switch. In my opinion, the black pawn does not have a choice between A4 and a4, but moves directly to A4 and captures the white pawn there.
I took the discussion from earlier to heart and to that extent I thought about it and adjusted the rules. The result:
I find the idea that a bishop on d1 can only move to a4 or to H5, or a bishop on e8 can only move to A4 or h5, to be completely illogical.
You can bend it with corners and sides so that it seems logical, but basically, from my point of view, it leads to complicating the rules.
The rule that a switch is a place of decision to occupy the squares of a switch uniquely, no matter from which direction the switch is occupied, seems to be a clear rule that everyone can understand. I do not think that such a rule complicates the course of the game.
The concept implies that unsymmetrical move sequences cannot be excluded. I cannot express it in any other way.
I now understand that a bishop from d1 can only reach H5 - sometimes it takes a little longer, sorry. G4 shares a side with h5 and so a move to h5 is not diagonal. But why can't a bishop from d1 move to A4 and what am I still overlooking here? B3 shares neither a side with a4 nor with A4. In this respect, a move from b3 to a4 is just as diagonal as a move from b3 to A4. If A4 is not possible, then a color change of the bishop from d1 via A4 to e8 is also not possible. Only the color change from e8 via A4 to d1 would be possible. The situation with the switch h5/H5 applies vice versa. What do I not realize here?
Should the description consider the following knight moves?
Knight on b3, is the move to a5 possible, because on the same diagonal? Or a knight on a3, are the moves to a5 or b5 possible, because on the same line?
Have read your explanations in Reroute66 and am now calmed down that from d1 a4 and A4 can be reached (was completely unsure for me before). In this respect, the color change of the bishop from d1 via A4 to e8 takes place (vice versa the situation from e8 to H5).
In the following constellation you show the possible moves of a knight in Reroute66.
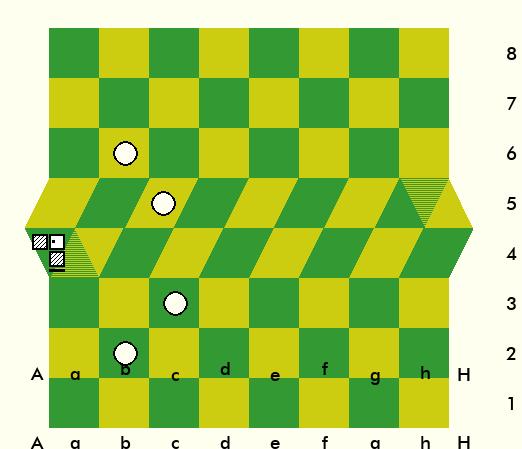
Is it possible that the move to d5 is missing here?
Who is Behind the Chess Variant Pages?. The editors, past editors, contributors, and inventors behind this site.[All Comments] [Add Comment or Rating]I added H. G. Muller as an editor and made a note about our inactive editors.
Dear H.G. Muller, can you be congratulated for joining the editorial circle? You have my congratulations.
May I ask if you want to continue to be rated as 'private' in an email contact? You are the only editor who has listed his email address as 'private' ( This member's email address is private).
It is certainly important for some users to be able to contact you directly. What do you mean?
Borderline. Without pawns, with only one king, capturing opponent's pieces is omitted. (7x7, Cells: 49) [All Comments] [Add Comment or Rating]I'll give it another try - even if that should mean a crack-up.
I have changed the rules, made it playable - hopefully!
It is not a 'big' game, a game for the short moment, something to exercise!
Whoever has improvements to contribute is very welcome.
Could this be an acceptable chess variant? Toggle Chess.
I would like to take this opportunity to remind you of my variant Borderline.
(Maybe not the most interesting variant, but it is quite suitable for a fast game.)
Borderline. Without pawns, with only one king, capturing opponent's pieces is omitted. (7x7, Cells: 49) [All Comments] [Add Comment or Rating]Do you mean white (er...blue?) pieces don't give check except when they are on ranks 4-7?
Almost - on the border line the king cannot be attacked. The king can be put in check only when a piece of one side has crossed the border line. Specifically, white (blue) can put the king in check on ranks 5-7, and black (red) can do so on ranks 3-1.
What do you think about the volatility of facing rooks and queens?
In Borderline, capturing pieces is excluded - except for the king, which must be captured to win the game. In this respect, it is not of particular importance when rooks and queens face each other. Did I understand the question correctly?
Why Boderline? Unlike the variants where the board is complexly changed (this also goes to my own address with Chess 66 or Chess 69) or new pieces with new move possibilities are created, I was looking for a mechanism which has a certain independence and which has not existed before (hopefully). Maybe I succeeded with a game where there is only one king, which both parties want to capture and which can be moved by both parties instead of one of their own pieces. It is also possible that the game has become too simple for many and they do not want to deal with it. We will see.
Okay Ben, sorry for the short rules section.
I added the rule about excluding capturing pieces to the rules section. If there is anything else missing from the rules section, please let me know.
I have played the game many times and did not get the impression that the queen and rook play a decisive role in the final result of the game.
If someone should take the pity to program the game, it will turn out that the strategic component of the game cannot be determined by single pieces.
In the rules I have emphasized: In contrast to all chess variants, the capturing of opposing pieces is excluded. Only the king can be captured.
Home page of The Chess Variant Pages. Homepage of The Chess Variant Pages.[All Comments] [Add Comment or Rating]Dear Fergus and dear authors of Chess Variant Pages,
perhaps I have not fully understood the Chess Variant Pages and do not know the possibilities that the system offers. Nevertheless, my question:
Is it conceivable - or already realized - to derive a ranking of attention or interest from the frequency of hits on a variant page? Such a possibility would be very helpful for the authors from my point of view to be able to recognize the appreciation of a variant.
I do not mean the Recognized Chess Variants in alphabetical order, nor the variants marked with 'hearts'. I have in mind a ranking in numerical ascending or descending order based on hits.
Did this already exist, so am I too late or is this an interesting approach?
Borderline. Without pawns, with only one king, capturing opponent's pieces is omitted. (7x7, Cells: 49) [All Comments] [Add Comment or Rating]My variant 'Borderline' is obviously ignored, although it has been published.
The reluctance is understandable.
Nevertheless, I would like to point out that the mechanism does not seem to have existed yet - does it? 'No pawns', 'the capture of pieces does not take place - except for the king'. This is against the holy grail. Agreed.
But why should only the most complicated variants get attention. And just those are made playable. It may be that I am in a dead end - but I would like to be able to understand that.
An honorable response, thank you.
... my hobby is programming computers, not playing games.
Would it cost you a lot of effort to program the variant? Maybe others would like to try the variant once. That would be then a beautiful conclusion.
I can understand that. It is a bit presumptuous of me to express such an idea.
But I'm glad to hear that the variant is treading a path that can hardly be compared. That also has something - at least for me. It was worth a try.
If the King can be captured, what stops the first player from using his Queen to capture the King and winning right away?
Winning in Borderline is like winning in classical chess. If the king is in check and cannot move away from it or use a piece of its own to protect it, it is checkmate and the game is over. If the situation is not checkmate, it is in the player's interest to move the king out of check (or use another piece to protect it), otherwise it will be captured on the opponent's next move and the game will be lost.
In Borderline, the king can be moved instead of one of your own pieces. It is not possible to move the king into your own check; such a move is not legal. The king can only be moved into check by another piece, not by a move of the king.
If the king is in check and could only be "saved" by a move into its own check - which is not possible/legal - then the player obliged to move has lost.
(here I have adapted my description again).
Impressive how the whole thing sounds from your point of view. Chapeau.
@Fergus
Before the queen can capture the king, the queen must first have put the king in check. And it can only do this when it has crossed the borderline. White queen (here blue) can only do this on ranks 5-7, black queen (here red) analogously on ranks 1-3.
Well, you must move the King into the other camp to be able to give check and checkmate.
Is that so? As soon as white has reached ranks 5-7 or black ranks 1-3, check or checkmate can be given. The king may not have moved until then.
Is it that a piece must be located on certain ranks to attack the King? Or is it that crossing the borderline results in a promotion that allows the piece to attack the King from anywhere on the board?
The former is the case. The possibility to attack is only possible beyond the borderline. Crossing the borderline has nothing to do with a promotion, which then applies to the entire board. The possibility to attack corresponds exclusively with the ranks 5-7 or 1-3.
While playing, I noticed the following:
Example 1
1st Rg5 Bf4 2nd Ne3 Bb4 (Rg5 is gone) 3rd Ra5 Nc5 (Ra5 is gone) 4th Qa4 Qd5 5th Nc3 Ne5 6th Nb5 Ne4 (Nb5 is gone) 7th Qc6 Nc4 (Qc6 is gone) 8th Nf5 Ne3 (Nf5 is gone)
Example 2:
1st Bb4 Bf4 2nd Bc5 Qd5 (Bc5 is gone) 3rd Qa4 Bb4 4th Qc6 Nc5 (Qc6 is gone) 5th Ne3 Ne5 6th Nf5 Ne4 (Nf5 is gone) and so on.
Works! Great, thank you.
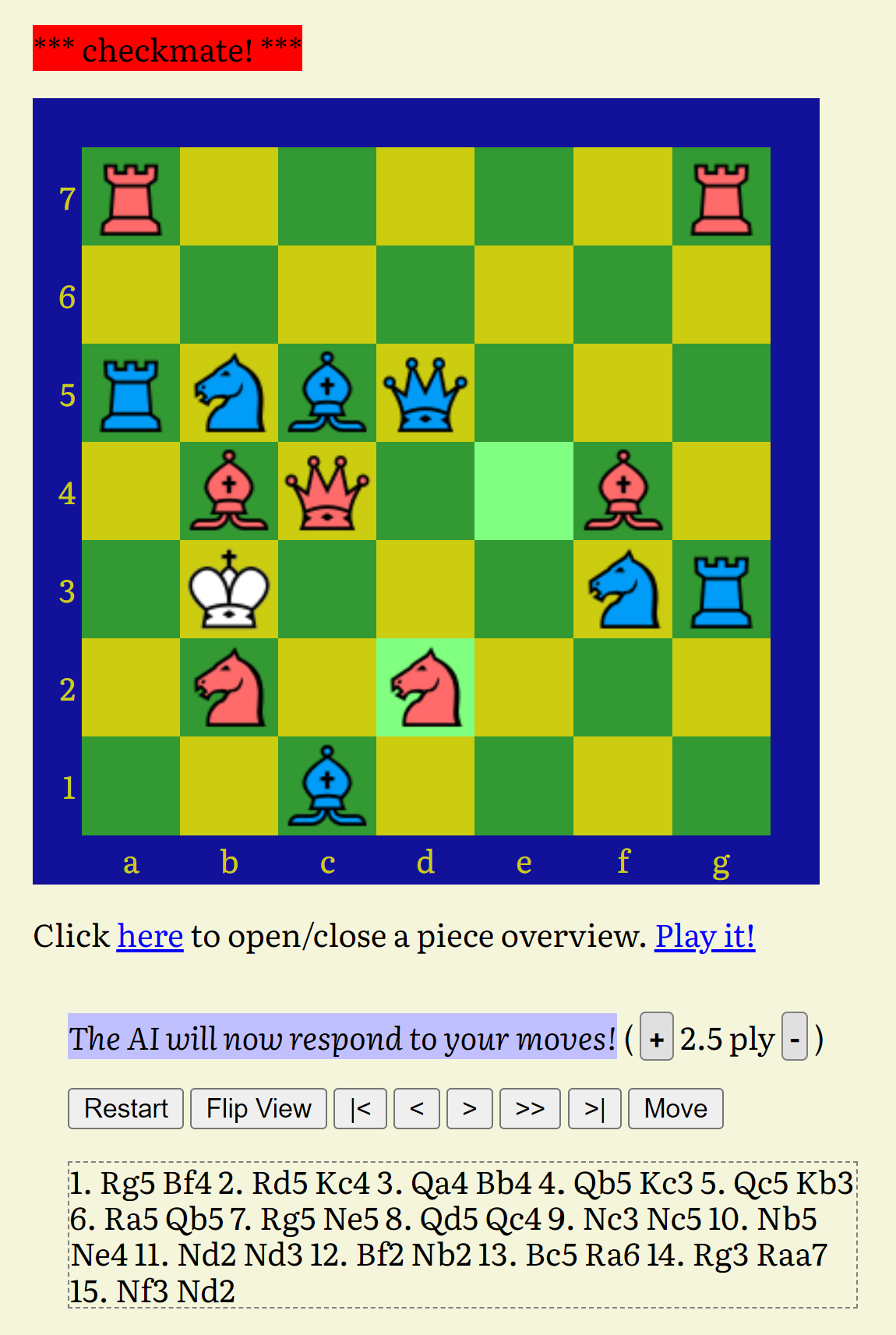
Plays well. For a game in between!
25 comments displayed
Permalink to the exact comments currently displayed.
The concept is expandable. At the maximum, it could look like this:
In this level, 16 new squares would be created. The game could then be called Chess 80, or in another notation Chess 64/16. Of course, intermediate levels between Chess 66 and Chess 80 are conceivable.
In the following example, moves can be made not only forked as in Chess 66, but triple-forked moves become possible.
Such an extended concept certainly leads to the question of playability. But it might be interesting to think about it.