Comments/Ratings for a Single Item

Right. So there is no path 4-a3-b2-c1. Which is what I meant, and needed to be said, because in the representation I had drawn, it looked like there could be.

I am still looking for a somewhat more intuitive description. It looks like 4 and a4 are really the same cell, (double width in my drawing), which always borders b4. And that there is a sliding door that either closes off the connection with a5 or b5, which has to be set as soon as you enter 4/a4, and can then not be altered until you leave it. (Which could be on the same turn.) Entering from above forces you to set the door such that you could enter.

Something doesn't work with this diagram. Maybe it is because only 2 colors are used, and a third one, neutral, should be used. Or because the triangular/losange doesn't work fine and something else has to be imagined.

I see the comments. It needs a lot of imagination to visualise something else and tell our brain that what we see is not right. What I see is simply a 66-cell board, where c1-b2-a3-4 is a diagonal, as well as 4-b5-c6-d7-e8, both being dark.

And a8-a7-a6-a5-4 is a column simply ending in 4. Like h1-h2-h3-h4-5, ending in 5.

That board only shifts the column (a to b, b to c, etc.) at the middle line. It doesn't change the color of the diagonals at all.

I understand the idea behind, but I think it needs to be worked more.

A somewhat simplified version of the same idea is this:

There is only a single, double-width cell a4 here, and there is no additional game state to distinguish between an occupant being in the right or left half of it. Moves (or move continuations) that leave a4 to 5th rank can choose whether they consider a5 or b5 the only square that connects to the upper edge of a4. So a4 has 2 'north' exits (to a5 and b5), two 'north-east' exits (to b5 and c5), and a single 'north-west' exit (to a5).

The difference with the rules that were given is that 'forward' moves even fork from a4, in addition to a1-a3.

How a Knight should move in the vicinity of the switch fields depends on which of the (normally equivalent) descriptions of Knight moves one adopts for the regular part of the board. The description "all two-step King moves that cannot be made by a Queen" is a rather unusual one; commonly one finds "one orthogonal King step followed by an outward diagonal one" (i.e. a non-lame Mao) or L-shaped "2 orthogonal steps plus a perpendicular one". Where the latter might also allow the move to start with the short leg. In my opinion the non-lame Mao description would be most intuitive here.

If I may summarize from my point of view:

I gather from the comments that my version is not easy to understand. But that's not a disadvantage a priori. It remains to be seen whether the possibility of checkmating the king with just one piece will play a role in chess. The same applies to the bishop, who can now change his color diagonal.

But if I see it correctly, then there are no bugs in the variant and the set of rules is consistent. Complicated, yes, but conclusive.

I gather from the comments that my version is not easy to understand.

I don't know if it's that or if you just haven't explained it clearly.

But if I see it correctly, then there are no bugs in the variant and the set of rules is consistent.

With respect to the Bishop, you told me that it can occupy only 4 or a4 or only 5 or h5. I presume the same holds for other pieces. So, a Rook on one of these spaces would not command two files. Likewise, a Knight on one of these spaces could not move as though it were on the other space. However, that looks like what the Knight is doing in your example. It's on 5, and its ability to move to f4 or g3 makes sense in light of that. But its ability to move to e4, f6 and g7 would make sense only if it were on h5 instead of 5.

I agree with your understanding Fergus. The best way to describe this geometry in a consistent manner for all pieces, remains to consider a4 and 4 (or h5 and 5) as a double cell. A piece on this double cell can be seen as being on both. Then, the diagram drawn by H.G. is fully correct.

a Knight on one of these spaces could not move as though it were on the other space. However, that looks like what the Knight is doing in your example

That much is clarified in the accompanying text. All three of e4, f6, and g7 can be reached by an orthogonal step (taking into account the rule about sideways moves from 5 going directly to g5) followed by a diagonal step.

This holds equally well whether we use the author's preferred definition for the knight move or either of the more common ones H.G. suggested

there are no bugs in the variant and the set of rules is consistent. Complicated, yes, but conclusive.

Afaict, the rules themselves are indeed consistent (and may well lead to an interesting game), but the explanation could be clearer, as shown by the fact that they seem to be unclear in some respect of another to most of the readers here.

Also I second H.G.'s request for clarification on the matter of knights moving through/over closed switches

I have begun to program Chess66 for Game Courier. So that 4 and 5 have separate file labels, I'm calling them A4 and H5 and distinguishing them from a5 and h5. I'm programming it with logical directions, which lets me define named directions as linked lists of nodes. The way directions are defined, the same direction cannot have two destinations from the same space. This means I've had to define additional directions to handle some lines of movement. However, the same direction can go from different spaces to the same destination.

One of the main difficulties I'm coming across is that sometimes it makes sense to treat A4 and a4 or H5 and h5 as separate spaces, and sometimes it makes sense to treat them as the same space. One idea would be to put an invisible dummy piece on the unoccupied space when the other one is occupied. That way, movement through a switch would be completely blocked.

At present, more work needs to be done to get the directions working properly.

Since a Bishop that moves to 4 could immediately switch to a4, is the reverse also true? Could a Bishop moving to a4 immediately switch to 4? More generally, is switching between these spaces available for any piece or only for Bishops?

The separation of the squares 4/a4 and h5/5 in the switches applies to all game pieces, including pawns.

Maybe I can clarify again from my point of view, especially for the knight:

A choice between the squares 4/a4 and h5/5 only goes in one direction. If a piece starts from a1/a2/a3 or from d1, c2 and so on, then there is a choice between squares 4 and a4, whereby the positioning must be clearly on 4 or a4. This means that the choice in a switch is only possible from 'below'. A rook/queen on the rank 4 can only occupy square a4 and not square 4. This applies to the switch h5/5 vice versa.

To clarify with the knight: A knight on 5 can move as shown in figure 10. Knights on g7 or f6 can occupy 5 or h5 because they come from 'below'. A knight on e4 can only reach h5 and not 5. A knight on g3 can only reach 5 but not h5. And a knight on f4 can move to 5 but not to h5.

This means that the squares of a switch are always seen separately and not partially as a same space.

It might be a bit difficult, but I hope it's consistent.

By what series of moves can a Bishop change to spaces of the other color?

Let me emphasize again: A change between 4 on a4 or h5 and 5 is not possible.

Some examples.

Bischoff on d1 to the left:

Standing on a4 after the move, a color transfer is not possible. Standing on 4 after the move, then a color transfer is possible. Because from there you can continue in the next move via b5, c6 etc., a color change has taken place.

Bishop on d1 to the right:

The move can go up to 5 (and not h5, this square cannot be occupied). The next move can be continued via g6, f7 etc. There has also been a color change.

For the other half of the board everything is vice versa.

Does that answer your question?

The more it's explained, the less I understand. The "a bit difficult" seems soft in my case. Here,

"Bishop on d1 to the right: The move can go up to 5 (and not h5, this square cannot be occupied). The next move can be continued via g6, f7 etc"

How come the Bishop goes from 5 to g6?

You said h5 cannot be occupied (by this Bishop I presume).

When the Bishop goes from 5 to g6, is it affected if another piece stands on h5?

Does that answer your question?

No, it does not. I specifically asked for a series of moves, and I didn't get that. What will answer my question is a series of moves in the generic rule-blind style of notation I used earlier. You do not have to write anything in English to answer this question.

a series of moves in the generic rule-blind style of notation I used earlier

The move sequences given by Gerd in his comment are B d1–4; B 4–b5 and B d1–5; B 5–g6. He also notes that B d1–h5 is not legal, but B d1–a4 is.

How come the Bishop goes from 5 to g6?

The top corners and the top and left sides are shared between h5 and 5, but the bottom side and corners are different. So 5 behaves as h5 from above (and cannot be occupied at the same time as it), and so is diagonally adjacent to g6.

When the Bishop goes from 5 to g6, is it affected if another piece stands on h5?

5 and h5 cannot be occupied simultaneously, so this situation does not arise. But since both are diagonally adjacent (by the same corner) to g6, it would presumably be fine if they could.

The move sequences given by Gerd in his comment are B d1–4; B 4–b5 and B d1–5; B 5–g6.

So, I gather that the following are all legal moves:

• B d1-4
• B 4-d1
• B e8-5
• B 5-e8

I think I misread an earlier answer. This actually describes one move on black spaces and the other move on white spaces:

If the bishop is on 4, then his path goes via b5, c6, d7 to e8. In the other direction it goes via b3, c2 to d1.

So, it looks like the diagonal from 4 to the first rank is a different color than 4, and the diagonal that goes from 5 to the last rank is a different color than 5, and that is how the color changing is done.

Suppose I have a Rook on d4. Could it move to 4? Or could it only move as far as a4? Likewise, could a Rook on d5 move to 5, or could it only move as far as g5?

I had already answered that before, as follows:

A rook/queen on the rank 4 can only occupy square a4 and not square 4. This applies to the switch h5/5 vice versa.

"So, I gather that the following are all legal moves:

B d1-4, B 4-d1, B e8-5, B 5-e8"

That is absolutely correct.

"So, it looks like the diagonal from 4 to the first rank is a different color than 4, and the diagonal that goes from 5 to the last rank is a different color than 5, and that is how the color changing is done."

By the way: The squares 4 and 5 do not have a uniform color. The squares are each composed of both colors. This is the only way to make a color change possible.

I try to follow. So a Rook cannot go from a4 to 4. And I understood that if there is a piece on a4, it is not possible to have another piece on 4.

At the end I wonder if this game is simply playable. I wouldn't be able to explain it to anyone I'm afraid.

I'm pretty sure that it would be possible to build something interesting on Gernd's idea by melting the cells a4 & 4, as well as h5 & 5. Which was similar to HG's diagram.

Doing this

• only 1 piece allowed on a4/4 or on h5/5
• a Rook on a1 would threat up to b8 AND a8 (as wished by Gernd)
• a Rook on h4 would threat up to a4/4
• a Bishop on d1 would go up to a4/4
• a Bishop on a4/4 would either go to f8 (keeping the color) or to d8 (switching the color).
• a Knight on a4/4 could go to b6, c5, a6, c6, b3, a2, b2, c3 (interesting)
• Chess 66 would have 64 cells which is maybe the real problem.

Dear En Bw, thank you for your comment, which is absolutely correct.

I'm testing my code for Chess66 on Game Courier right now, and with a Knight on a3, I currently have its legal moves as a5, c5, c4, c2, and b1. Because 4 is right above it, it looks like b5 could be another legal move by going over 4 and a5 and turning right to b5. It could be argued that this is illegal because there is a single-direction path from a3 to b5. But if that rules that out, it might also rule out a5 as a legal move, because there is a single-direction path to it through 4.

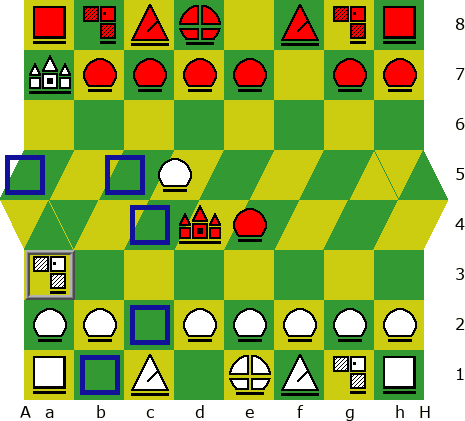
I don't think that the moves to a5 and b5 are legal since they are on the same line. Merging the squares 4 and a4 would not change that. On the contrary, the possibility of being able to detect movements on the same line or the same diagonal would be diluted.

A rook/queen on the rank 4 can only occupy square a4 and not square 4. This applies to the switch h5/5 vice versa.

That's interesting; given that a rook is allowed to move sideways from 4 onto b4 and beyond, that means that a rook on 4 can threaten a rook on b4 without being attacked back. Is this intentional?

The squares 4 and 5 do not have a uniform color. The squares are each composed of both colors.

Strictly speaking, the colours on the squares are a representational convention and bear no real influence on the game; ‘a bishop can change colour’ is equivalent to saying a bishop can reach the whole board, or in other words all squares are effectively the same colour. But that's a minor quibble

En Bw

I assume you mean me? That's one correct letter out of four, with two more misplaced ;)

I don't think that the moves to a5 and b5 are legal since they are on the same line.

That's one of the few things which changes depending on the knight‐move definition; the definition you've chosen would indeed exclude both destinations, as a queen can reach both of those squares; but the more usual definitions H.G. first brought up (either two othrogonal steps in one direction and one at right angles, or (my preferred expression) one orthogonal and one diagonally outwards — in either order (or not…?) and for some suitable definition of ‘outwards’) would probably allow both moves. Equally the question of whether N h4–g6 is legal, and probably other similar moves, is implicated there. There may be some way of defining the knight move to include only a subset of the moves in question, but that's unltimately for Gerd to decide if he wants to look for (or someone else to contribute if they come up w/ sth).